ビジネスでもスポーツでも恋愛でも、対立する「ライバル」や協力してくれる「仲間」がいるのがこの世の中。そして、競い合う相手や仲間が存在することを前提に、会社の経営や経済、社会の制度設計などを研究するのが「ゲーム理論」です。今回はゲーム理論について解説します。
「ゲーム理論」とは?
「ゲーム理論」とは、利害関係のある相手がいる中で、自分と相手、それぞれの利益を分析して、最適な行動を決めるための思考方法です。現実のビジネスや人間社会は、複数の人間、会社、組織が関わりながら進んでいます。そこで、相手の動き、仲間の動きを「ゲーム」に見立てたうえで、数学的なアプローチを活用しつつ、対策を導き出すわけです。
ゲーム理論は1994年、数学者であるジョン・フォン・ノイマン、経済学者であるオスカー・モルゲンシュテルンによって書かれた『ゲームの理論と経済行動』に始まるとされています。
その数学者と経済学者によって書かれたことからも想像がつくとおり、ゲーム理論はもともと「数学」と「経済学」から生まれたものです。しかし今では、経営や政治、心理学、生物学、工学など、さまざまな領域でも応用されています。
仲間を信じるべきか、裏切るべきか? 「囚人のジレンマ」
ゲーム理論の説明によく取り上げられるのが「囚人のジレンマ」です。これは、同じ犯罪に関わった2人の囚人に対する取り調べを使った例え話で、次のような矛盾を含んでいます。
囚人は別々に取り調べを受けており、連絡を取り合うことはできません。その状況で調査官は囚人に司法取引を持ちかけます。それは次のような条件でした。
- 2人とも自白したら、2人は懲役5年
- 2人とも黙秘を続けたら、2人は懲役2年
- 1人だけが自白したら、自白したほうは無罪、黙秘したほうは懲役10年
それぞれの利得を追求する「ナッシュ均衡」
さて、このとき囚人はどう行動するのが最適でしょうか? 囚人の選択肢には「自白する/自白しない」の二つしかありません。
<自分が自白した場合>
共犯者が黙秘した場合は、自分は無罪になる。ただし共犯者も自白した場合は、2人とも懲役5年になってしまう。
<自分が黙秘した場合>
共犯者も黙秘した場合は、2人とも懲役2年に。しかし、共犯者が自白した場合は、自分だけが懲役10年なってしまう。
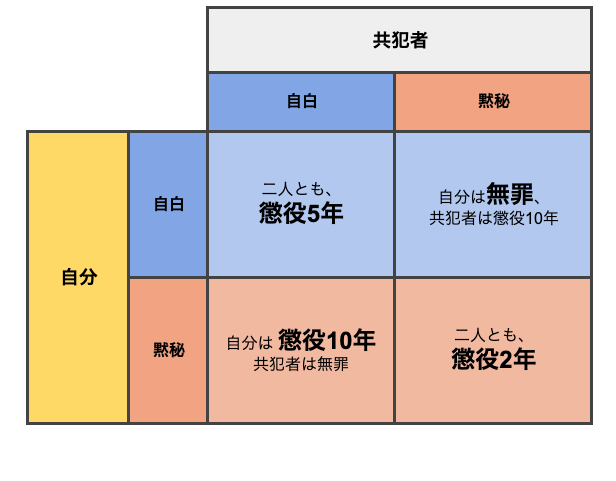
囚人にとっての最悪は懲役10年になること。そのリスクを避けるには「自白」するのが確実です。ゲーム理論ではこのように、自分にとって合理的な行動をとることを「ナッシュ均衡」と呼びます。
しかし、互いを信じて「黙秘」を貫けば、2人とも懲役2年になります。全体の利得を追求するなら、黙秘がもっともよい選択となりますが、「懲役10年だけは避けたい」と考えると、なかなかそういう選択はできません。
<模擬講義「ゲーム理論で理解する世の中のしくみ」:東京理科大学>
コロナ禍でのマスク争奪戦に見るゲーム理論
このように、個人の利得と全体の利得が相反することは、この世の中にたくさんあります。例えば、新型コロナウイルス感染症が広がったときに、マスクやトイレットペーパーが売り切れになり、手に入りにくくなるという状況が生まれました。
これなどはまさにゲーム理論の典型といえるでしょう。マスクを買い占めることは個人にとっての利得を追求したナッシュ均衡になりますが、社会全体のメリットにはなりません。
ビジネスでは、企業の利得を優先するのが当たり前
ゲーム理論では「ナッシュ均衡が悪い」といっているわけではありません。マスクの例でいえば、各個人が自分の利得を合理的に考えれば、買い占めという行動が起こるのは当然のことであり、それを前提に考えるのがゲーム理論のアプローチです。
また当然、個々の利得を追求しても問題ない場面もあります。特にライバル企業との競争に常にさらされるビジネスにおいては、「相手の出方を分析しながら、最適な一手を選択する」ことがポイントになります。そのようなときに、「この場面においてのナッシュ均衡はどこか?」を見極めて検討することは重要です。
注目されている「マーケットデザイン」
ゲーム理論はすでにいろいろな領域で使われ始めていますが、中でも最近注目されているのが、「マーケットデザイン」と呼ばれる領域です。マーケットデザインとは、ゲーム理論を用いて社会の新しい制度を考えようというものです。
そのなかでも「マッチング理論」が、社会制度の改革に役立つものとして実用化されています。いくつか例を紹介します。
研修医マッチング
これは、研修医制度でのマッチングです。医学生は研修医として、実際の病院で働きながら医学の知識やスキルを高めていきます。このとき、「医学生が行きたいと望む病院」と「病院側が求める医学生」が必ずしも一致するとは限りません。
そこでゲーム理論を用いて、医学生と病院側の希望を調整するシステムが設計されました。日本では「医師臨床研修マッチング協議会」が両者の希望を集約し、コンピューターのアルゴリズムを用いてマッチングしています。
医師臨床研修マッチング協議会
https://www.jrmp.jp/
学校選択制
学校選択制では、かつては「本当は人気の高い学校に行きたいが、抽選に漏れると困るから、人気の少ないところを第一希望にしておこう」というように、本来の希望を偽って申請するケースも見受けられました。
しかしゲーム理論を活用したところでは、希望を偽ったりせずに、全員が第一希望で申請しても不利益を被らない仕組みに変わりました(全員が第一希望に行けるという意味ではありません)。
その他、期待される分野
その他にも、保育所の待機児童問題、企業内の人事採用や人事異動、中途採用、臓器移植などにもマーケットデザインが活用できると期待されています。
「ゲーム理論」を学べる大学の学部、学科
ゲーム理論は数学と経済学から始まった学問であり(この記事では分かりやすいように数学、数式については触れずに解説しましたが)、本来は数学を用います。ゲーム理論そのものを研究したい場合は数学を専門とする学部、応用については経済学部が適しているといえます。
しかし、ゲーム理論はさまざまな分野で活用できるものです。「会社を経営したいので、ゲーム理論も理解しておきたい」というような場合は経営学部など、「モノづくりにゲーム理論を応用したい」という場合は工学系の学部でも学べます。
また東京大学「マーケットデザインセンター(UTMD)」、慶應義塾大学 経済研究所「マーケットデザイン研究センター(SIMDI)」のような拠点を持つところであれば、より深く学ぶことができるでしょう。
東京大学「マーケットデザインセンター(UTMD)」
https://www.mdc.e.u-tokyo.ac.jp/
慶應義塾大学 経済研究所「マーケットデザイン研究センター(SIMDI)」
https://ies.keio.ac.jp/attached-center/simdi/
企業経営、人事、転職や中途採用、マッチング、教育、医療、災害対策など






















